Analyze Xenium data

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
import seaborn as sns

import scanpy as sc
import squidpy as sq

Download the Feature-cell Matrix (HDF5) and the Cell summary file (CSV) from the Xenium breast cancer tumor microenvironment Dataset.

You need these 2 files in a new folder tutorial_data in the same path as your notebook.

• Xenium_FFPE_Human_Breast_Cancer_Rep1_cell_feature_matrix.h5

• Xenium_FFPE_Human_Breast_Cancer_Rep1_cells.csv

The following lines create the folder structure which can be used to load the data.

# !mkdir tutorial_data
# !mkdir tutorial_data/xenium_data
# !wget -P tutorial_data/xenium_data/ https://cf.10xgenomics.com/samples/xenium/preview/Xenium_FFPE_Human_Breast_Cancer_Rep1/Xenium_FFPE_Human_Breast_Cancer_Rep1_cell_feature_matrix.h5
# !wget -P tutorial_data/xenium_data/ https://cf.10xgenomics.com/samples/xenium/preview/Xenium_FFPE_Human_Breast_Cancer_Rep1/Xenium_FFPE_Human_Breast_Cancer_Rep1_cells.csv.gz
# !tar -xzf tutorial_data/xenium_data/Xenium_FFPE_Human_Breast_Cancer_Rep1_cells.csv.gz -C tutorial_data/xenium_data/

adata = sc.read_10x_h5(
    filename="tutorial_data/xenium_data/Xenium_FFPE_Human_Breast_Cancer_Rep1_cell_feature_matrix.h5"
)

df = pd.read_csv(
    "tutorial_data/xenium_data/Xenium_FFPE_Human_Breast_Cancer_Rep1_cells.csv"
)

df.set_index(adata.obs_names, inplace=True)
adata.obs = df.copy()

adata.obsm["spatial"] = adata.obs[["x_centroid", "y_centroid"]].copy().to_numpy()

adata.obs

	cell_id	x_centroid	y_centroid	transcript_counts	control_probe_counts	control_codeword_counts	total_counts	cell_area	nucleus_area	n_genes_by_counts	log1p_n_genes_by_counts	log1p_total_counts	pct_counts_in_top_10_genes	pct_counts_in_top_20_genes	pct_counts_in_top_50_genes	pct_counts_in_top_150_genes
1	1	377.663005	843.541888	154	0	0	154.0	110.361875	45.562656	62	4.143135	5.043425	55.844156	71.428571	92.207792	100.0
2	2	382.078658	858.944818	64	0	0	64.0	87.919219	24.248906	40	3.713572	4.174387	48.437500	68.750000	100.000000	100.0
3	3	319.839529	869.196542	57	0	0	57.0	52.561875	23.526406	41	3.737670	4.060443	43.859649	63.157895	100.000000	100.0
4	4	259.304707	851.797949	120	0	0	120.0	75.230312	35.176719	50	3.931826	4.795791	49.166667	71.666667	100.000000	100.0
5	5	370.576291	865.193024	120	0	0	120.0	180.218594	34.499375	65	4.189655	4.795791	42.500000	62.500000	87.500000	100.0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
167778	167778	7455.404785	5115.021094	238	1	0	238.0	219.956094	61.412500	77	4.356709	5.476463	43.277311	63.445378	88.655462	100.0
167779	167779	7483.771045	5111.720703	80	0	0	80.0	38.427969	25.964844	36	3.610918	4.394449	55.000000	80.000000	100.000000	100.0
167780	167780	7470.119580	5119.350366	406	0	0	406.0	287.690469	86.158125	75	4.330733	6.008813	55.911330	73.152709	93.842365	100.0
167781	167781	7477.704004	5128.963086	120	0	0	120.0	235.670469	25.016563	52	3.970292	4.795791	47.500000	70.000000	98.333333	100.0
167782	167782	7489.376562	5123.402393	393	0	0	393.0	269.447344	111.445625	78	4.369448	5.976351	45.292621	69.465649	92.875318	100.0

167782 rows × 16 columns

Calculate quality control metrics

Calculate the quality control metrics on the anndata.AnnData using scanpy.pp.calculate_qc_metrics.

sc.pp.calculate_qc_metrics(adata, percent_top=(10, 20, 50, 150), inplace=True)

The percentage of control probes and control codewords can be calculated from adata.obs

cprobes = (
    adata.obs["control_probe_counts"].sum() / adata.obs["total_counts"].sum() * 100
)
cwords = (
    adata.obs["control_codeword_counts"].sum() / adata.obs["total_counts"].sum() * 100
)
print(f"Negative DNA probe count % : {cprobes}")
print(f"Negative decoding count % : {cwords}")

Negative DNA probe count % : 0.08700852649698224
Negative decoding count % : 0.005482476054877954

Next we plot the distribution of total transcripts per cell, unique transcripts per cell, area of segmented cells and the ratio of nuclei area to their cells

fig, axs = plt.subplots(1, 4, figsize=(15, 4))

axs[0].set_title("Total transcripts per cell")
sns.histplot(
    adata.obs["total_counts"],
    kde=False,
    ax=axs[0],
)

axs[1].set_title("Unique transcripts per cell")
sns.histplot(
    adata.obs["n_genes_by_counts"],
    kde=False,
    ax=axs[1],
)


axs[2].set_title("Area of segmented cells")
sns.histplot(
    adata.obs["cell_area"],
    kde=False,
    ax=axs[2],
)

axs[3].set_title("Nucleus ratio")
sns.histplot(
    adata.obs["nucleus_area"] / adata.obs["cell_area"],
    kde=False,
    ax=axs[3],
)

<AxesSubplot: title={'center': 'Nucleus ratio'}, ylabel='Count'>

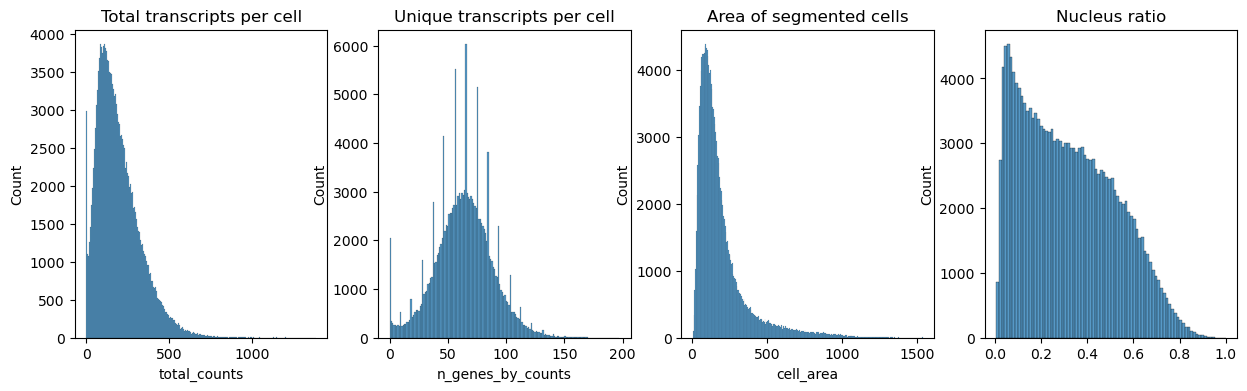
Filter the cells based on the minimum number of counts required using scanpy.pp.filter_cells. Filter the genes based on the minimum number of cells required with scanpy.pp.filter_genes. The parameters for the both were specified based on the plots above. They were set to filter out the cells and genes with minimum counts and minimum cells respectively.

Other filter criteria might be cell area, DAPI signal or a minimum of unique transcripts.

sc.pp.filter_cells(adata, min_counts=10)
sc.pp.filter_genes(adata, min_cells=5)

Normalize counts per cell using scanpy.pp.normalize_total.

Logarithmize, do principal component analysis, compute a neighborhood graph of the observations using scanpy.pp.log1p, scanpy.pp.pca and scanpy.pp.neighbors respectively.

Use scanpy.tl.umap to embed the neighborhood graph of the data and cluster the cells into subgroups employing scanpy.tl.leiden.

adata.layers["counts"] = adata.X.copy()
sc.pp.normalize_total(adata, inplace=True)
sc.pp.log1p(adata)
sc.pp.pca(adata)
sc.pp.neighbors(adata)
sc.tl.umap(adata)
sc.tl.leiden(adata)

c:\Users\laure\AppData\Local\Programs\Python\Python310\lib\site-packages\tqdm\auto.py:22: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm

Visualize annotation on UMAP and spatial coordinates

Subplot with scatter plot in UMAP (Uniform Manifold Approximation and Projection) basis. The embedded points were colored, respectively, according to the total counts, number of genes by counts, and leiden clusters in each of the subplots. This gives us some idea of what the data looks like.

sc.pl.umap(
    adata,
    color=[
        "total_counts",
        "n_genes_by_counts",
        "leiden",
    ],
    wspace=0.4,
)

sq.pl.spatial_scatter(
    adata,
    library_id="spatial",
    shape=None,
    color=[
        "leiden",
    ],
    wspace=0.4,
)

Computation of spatial statistics

Building the spatial neighbors graphs

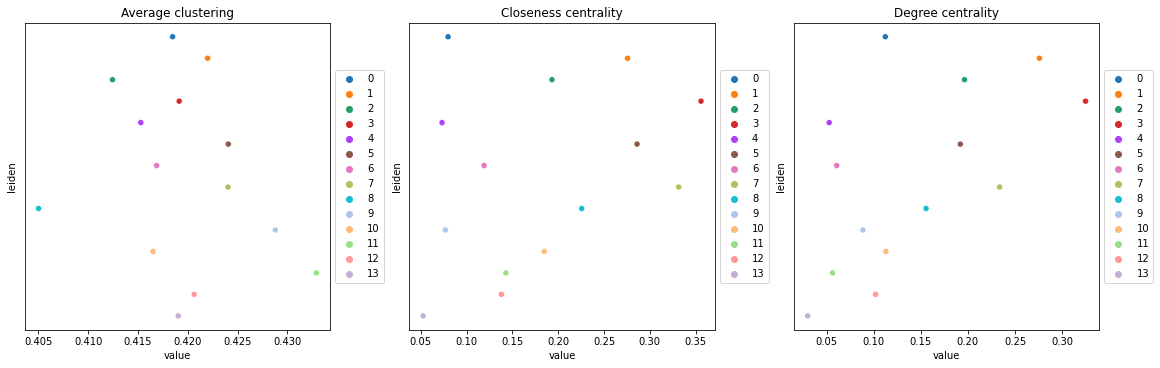
This example shows how to compute centrality scores, given a spatial graph and cell type annotation.

The scores calculated are closeness centrality, degree centrality and clustering coefficient with the following properties:

• closeness centrality - measure of how close the group is to other nodes.

• clustering coefficient - measure of the degree to which nodes cluster together.

• degree centrality - fraction of non-group members connected to group members.

All scores are descriptive statistics of the spatial graph.

This dataset contains Leiden cluster groups’ annotations in anndata.AnnData.obs, which are used for calculation of centrality scores.

First, we need to compute a connectivity matrix from spatial coordinates to calculate the centrality scores. We can use squidpy.gr.spatial_neighbors for this purpose. We use the coord_type="generic" based on the data and the neighbors are classified with Delaunay triangulation by specifying delaunay=True.

sq.gr.spatial_neighbors(adata, coord_type="generic", delaunay=True)

Compute centrality scores

Centrality scores are calculated with squidpy.gr.centrality_scores, with the Leiden groups as clusters.

sq.gr.centrality_scores(adata, cluster_key="leiden")

The results were visualized by plotting the average centrality, closeness centrality, and degree centrality using squidpy.pl.centrality_scores.

sq.pl.centrality_scores(adata, cluster_key="leiden", figsize=(16, 5))

Compute co-occurrence probability

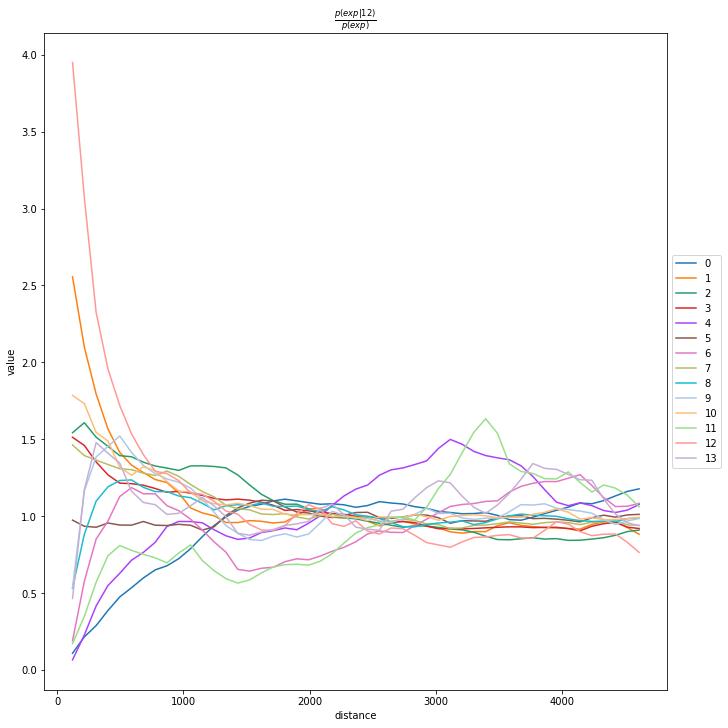
This example shows how to compute the co-occurrence probability.

The co-occurrence score is defined as:

(1)\[\begin{equation} \frac{p(exp|cond)}{p(exp)} \end{equation}\]

where \(p(exp|cond)\) is the conditional probability of observing a cluster \(exp\) conditioned on the presence of a cluster \(cond\), whereas \(p(exp)\) is the probability of observing \(exp\) in the radius size of interest. The score is computed across increasing radii size around each cell in the tissue.

We can compute the co-occurrence score with squidpy.gr.co_occurrence. Results of co-occurrence probability ratio can be visualized with squidpy.pl.co_occurrence. The ‘3’ in the \(\frac{p(exp|cond)}{p(exp)}\) represents a Leiden clustered group.

We can further visualize tissue organization in spatial coordinates with squidpy.pl.spatial_scatter, with an overlay of the expressed genes which were colored in consonance with the Leiden clusters.

adata_subsample = sc.pp.subsample(adata, fraction=0.5, copy=True)

sq.gr.co_occurrence(
    adata_subsample,
    cluster_key="leiden",
)
sq.pl.co_occurrence(
    adata_subsample,
    cluster_key="leiden",
    clusters="12",
    figsize=(10, 10),
)
sq.pl.spatial_scatter(
    adata_subsample,
    color="leiden",
    shape=None,
    size=2,
)

WARNING: `n_splits` was automatically set to `41` to prevent `82039x82039` distance matrix from being created

100%|██████████| 861/861 [15:08<00:00,  1.06s/]

WARNING: Please specify a valid `library_id` or set it permanently in `adata.uns['spatial']`

Neighbors enrichment analysis

This example shows how to run the neighbors enrichment analysis routine.

It calculates an enrichment score based on proximity on the connectivity graph of cell clusters. The number of observed events is compared against \(N\) permutations and a z-score is computed.

This dataset contains cell type annotations in anndata.Anndata.obs which are used for calculation of the neighborhood enrichment. We calculate the neighborhood enrichment score with squidpy.gr.nhood_enrichment.

sq.gr.nhood_enrichment(adata, cluster_key="leiden")

100%|██████████| 1000/1000 [00:25<00:00, 38.50/s]

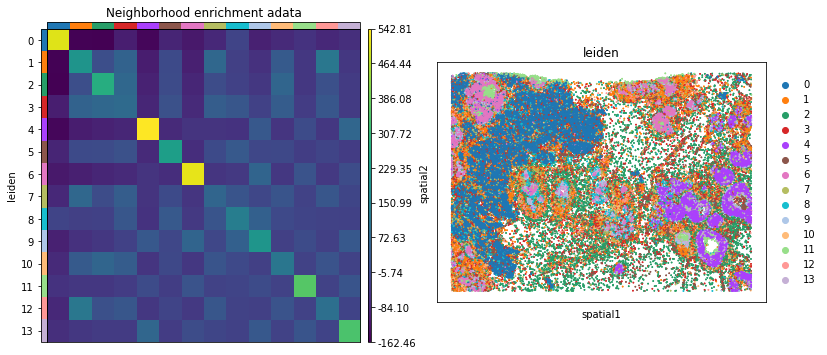
And visualize the results with squidpy.pl.nhood_enrichment.

fig, ax = plt.subplots(1, 2, figsize=(13, 7))
sq.pl.nhood_enrichment(
    adata,
    cluster_key="leiden",
    figsize=(8, 8),
    title="Neighborhood enrichment adata",
    ax=ax[0],
)
sq.pl.spatial_scatter(adata_subsample, color="leiden", shape=None, size=2, ax=ax[1])

WARNING: Please specify a valid `library_id` or set it permanently in `adata.uns['spatial']`

Compute Moran’s I score

This example shows how to compute the Moran’s I global spatial auto-correlation statistics.

The Moran’s I global spatial auto-correlation statistics evaluates whether features (i.e. genes) shows a pattern that is clustered, dispersed or random in the tissue are under consideration.

We can compute the Moran’s I score with squidpy.gr.spatial_autocorr and mode = 'moran'. We first need to compute a spatial graph with squidpy.gr.spatial_neighbors. We will also subset the number of genes to evaluate.

sq.gr.spatial_neighbors(adata_subsample, coord_type="generic", delaunay=True)
sq.gr.spatial_autocorr(
    adata_subsample,
    mode="moran",
    n_perms=100,
    n_jobs=1,
)
adata_subsample.uns["moranI"].head(10)

100%|██████████| 100/100 [34:39<00:00, 20.80s/]

	I	pval_norm	var_norm	pval_z_sim	pval_sim	var_sim	pval_norm_fdr_bh	pval_z_sim_fdr_bh	pval_sim_fdr_bh
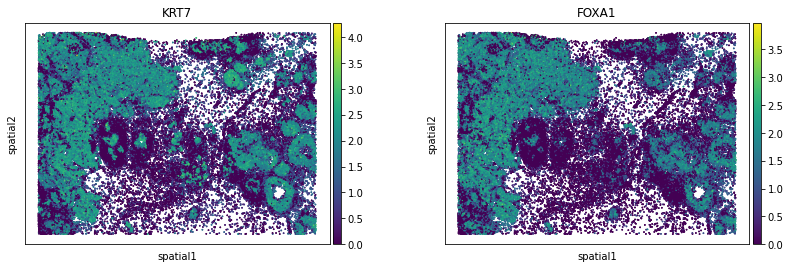
KRT7	0.696668	0.0	0.000004	0.0	0.009901	0.000008	0.0	0.0	0.009965
SCD	0.671975	0.0	0.000004	0.0	0.009901	0.000009	0.0	0.0	0.009965
FOXA1	0.659014	0.0	0.000004	0.0	0.009901	0.000008	0.0	0.0	0.009965
FASN	0.653400	0.0	0.000004	0.0	0.009901	0.000006	0.0	0.0	0.009965
EPCAM	0.641954	0.0	0.000004	0.0	0.009901	0.000009	0.0	0.0	0.009965
TACSTD2	0.638978	0.0	0.000004	0.0	0.009901	0.000007	0.0	0.0	0.009965
CEACAM6	0.631554	0.0	0.000004	0.0	0.009901	0.000009	0.0	0.0	0.009965
ERBB2	0.628083	0.0	0.000004	0.0	0.009901	0.000009	0.0	0.0	0.009965
KRT8	0.619555	0.0	0.000004	0.0	0.009901	0.000008	0.0	0.0	0.009965
LUM	0.593700	0.0	0.000004	0.0	0.009901	0.000007	0.0	0.0	0.009965

We can visualize some of those genes with squidpy.pl.spatial_scatter. We could also pass mode = 'geary' to compute a closely related auto-correlation statistic, Geary’s C. See squidpy.gr.spatial_autocorr for more information.

sq.pl.spatial_scatter(
    adata_subsample,
    library_id="spatial",
    color=[
        "KRT7",
        "FOXA1",
    ],
    shape=None,
    size=2,
    img=False,
)