Analyze Xenium data
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scanpy as sc
import squidpy as sq
Download the Feature-cell Matrix (HDF5) and the Cell summary file (CSV) from the Xenium breast cancer tumor microenvironment Dataset.
You need these 2 files in a new folder tutorial_data in the same path as your notebook.
Xenium_FFPE_Human_Breast_Cancer_Rep1_cell_feature_matrix.h5Xenium_FFPE_Human_Breast_Cancer_Rep1_cells.csv
The following lines create the folder structure which can be used to load the data.
# !mkdir tutorial_data
# !mkdir tutorial_data/xenium_data
# !wget -P tutorial_data/xenium_data/ https://cf.10xgenomics.com/samples/xenium/preview/Xenium_FFPE_Human_Breast_Cancer_Rep1/Xenium_FFPE_Human_Breast_Cancer_Rep1_cell_feature_matrix.h5
# !wget -P tutorial_data/xenium_data/ https://cf.10xgenomics.com/samples/xenium/preview/Xenium_FFPE_Human_Breast_Cancer_Rep1/Xenium_FFPE_Human_Breast_Cancer_Rep1_cells.csv.gz
# !tar -xzf tutorial_data/xenium_data/Xenium_FFPE_Human_Breast_Cancer_Rep1_cells.csv.gz -C tutorial_data/xenium_data/
adata = sc.read_10x_h5(
filename="tutorial_data/xenium_data/Xenium_FFPE_Human_Breast_Cancer_Rep1_cell_feature_matrix.h5"
)
df = pd.read_csv(
"tutorial_data/xenium_data/Xenium_FFPE_Human_Breast_Cancer_Rep1_cells.csv"
)
df.set_index(adata.obs_names, inplace=True)
adata.obs = df.copy()
adata.obsm["spatial"] = adata.obs[["x_centroid", "y_centroid"]].copy().to_numpy()
adata.obs
| cell_id | x_centroid | y_centroid | transcript_counts | control_probe_counts | control_codeword_counts | total_counts | cell_area | nucleus_area | n_genes_by_counts | log1p_n_genes_by_counts | log1p_total_counts | pct_counts_in_top_10_genes | pct_counts_in_top_20_genes | pct_counts_in_top_50_genes | pct_counts_in_top_150_genes | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 377.663005 | 843.541888 | 154 | 0 | 0 | 154.0 | 110.361875 | 45.562656 | 62 | 4.143135 | 5.043425 | 55.844156 | 71.428571 | 92.207792 | 100.0 |
| 2 | 2 | 382.078658 | 858.944818 | 64 | 0 | 0 | 64.0 | 87.919219 | 24.248906 | 40 | 3.713572 | 4.174387 | 48.437500 | 68.750000 | 100.000000 | 100.0 |
| 3 | 3 | 319.839529 | 869.196542 | 57 | 0 | 0 | 57.0 | 52.561875 | 23.526406 | 41 | 3.737670 | 4.060443 | 43.859649 | 63.157895 | 100.000000 | 100.0 |
| 4 | 4 | 259.304707 | 851.797949 | 120 | 0 | 0 | 120.0 | 75.230312 | 35.176719 | 50 | 3.931826 | 4.795791 | 49.166667 | 71.666667 | 100.000000 | 100.0 |
| 5 | 5 | 370.576291 | 865.193024 | 120 | 0 | 0 | 120.0 | 180.218594 | 34.499375 | 65 | 4.189655 | 4.795791 | 42.500000 | 62.500000 | 87.500000 | 100.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 167778 | 167778 | 7455.404785 | 5115.021094 | 238 | 1 | 0 | 238.0 | 219.956094 | 61.412500 | 77 | 4.356709 | 5.476463 | 43.277311 | 63.445378 | 88.655462 | 100.0 |
| 167779 | 167779 | 7483.771045 | 5111.720703 | 80 | 0 | 0 | 80.0 | 38.427969 | 25.964844 | 36 | 3.610918 | 4.394449 | 55.000000 | 80.000000 | 100.000000 | 100.0 |
| 167780 | 167780 | 7470.119580 | 5119.350366 | 406 | 0 | 0 | 406.0 | 287.690469 | 86.158125 | 75 | 4.330733 | 6.008813 | 55.911330 | 73.152709 | 93.842365 | 100.0 |
| 167781 | 167781 | 7477.704004 | 5128.963086 | 120 | 0 | 0 | 120.0 | 235.670469 | 25.016563 | 52 | 3.970292 | 4.795791 | 47.500000 | 70.000000 | 98.333333 | 100.0 |
| 167782 | 167782 | 7489.376562 | 5123.402393 | 393 | 0 | 0 | 393.0 | 269.447344 | 111.445625 | 78 | 4.369448 | 5.976351 | 45.292621 | 69.465649 | 92.875318 | 100.0 |
167782 rows × 16 columns
Calculate quality control metrics
Calculate the quality control metrics on the anndata.AnnData using scanpy.pp.calculate_qc_metrics.
sc.pp.calculate_qc_metrics(adata, percent_top=(10, 20, 50, 150), inplace=True)
The percentage of control probes and control codewords can be calculated from adata.obs
cprobes = (
adata.obs["control_probe_counts"].sum() / adata.obs["total_counts"].sum() * 100
)
cwords = (
adata.obs["control_codeword_counts"].sum() / adata.obs["total_counts"].sum() * 100
)
print(f"Negative DNA probe count % : {cprobes}")
print(f"Negative decoding count % : {cwords}")
Negative DNA probe count % : 0.08700852649698224
Negative decoding count % : 0.005482476054877954
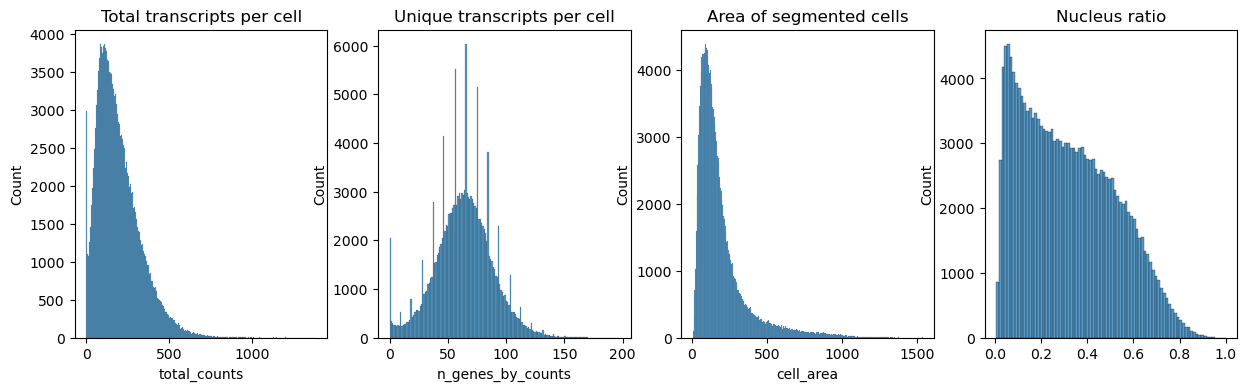
Next we plot the distribution of total transcripts per cell, unique transcripts per cell, area of segmented cells and the ratio of nuclei area to their cells
fig, axs = plt.subplots(1, 4, figsize=(15, 4))
axs[0].set_title("Total transcripts per cell")
sns.histplot(
adata.obs["total_counts"],
kde=False,
ax=axs[0],
)
axs[1].set_title("Unique transcripts per cell")
sns.histplot(
adata.obs["n_genes_by_counts"],
kde=False,
ax=axs[1],
)
axs[2].set_title("Area of segmented cells")
sns.histplot(
adata.obs["cell_area"],
kde=False,
ax=axs[2],
)
axs[3].set_title("Nucleus ratio")
sns.histplot(
adata.obs["nucleus_area"] / adata.obs["cell_area"],
kde=False,
ax=axs[3],
)
Filter the cells based on the minimum number of counts required using scanpy.pp.filter_cells. Filter the genes based on the minimum number of cells required with scanpy.pp.filter_genes. The parameters for the both were specified based on the plots above. They were set to filter out the cells and genes with minimum counts and minimum cells respectively.
Other filter criteria might be cell area, DAPI signal or a minimum of unique transcripts.
sc.pp.filter_cells(adata, min_counts=10)
sc.pp.filter_genes(adata, min_cells=5)
Normalize counts per cell using scanpy.pp.normalize_total.
Logarithmize, do principal component analysis, compute a neighborhood graph of the observations using scanpy.pp.log1p, scanpy.pp.pca and scanpy.pp.neighbors respectively.
Use scanpy.tl.umap to embed the neighborhood graph of the data and cluster the cells into subgroups employing scanpy.tl.leiden.
adata.layers["counts"] = adata.X.copy()
sc.pp.normalize_total(adata, inplace=True)
sc.pp.log1p(adata)
sc.pp.pca(adata)
sc.pp.neighbors(adata)
sc.tl.umap(adata)
sc.tl.leiden(adata)
c:\Users\laure\AppData\Local\Programs\Python\Python310\lib\site-packages\tqdm\auto.py:22: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
Visualize annotation on UMAP and spatial coordinates
Subplot with scatter plot in UMAP (Uniform Manifold Approximation and Projection) basis. The embedded points were colored, respectively, according to the total counts, number of genes by counts, and leiden clusters in each of the subplots. This gives us some idea of what the data looks like.
Computation of spatial statistics
Building the spatial neighbors graphs
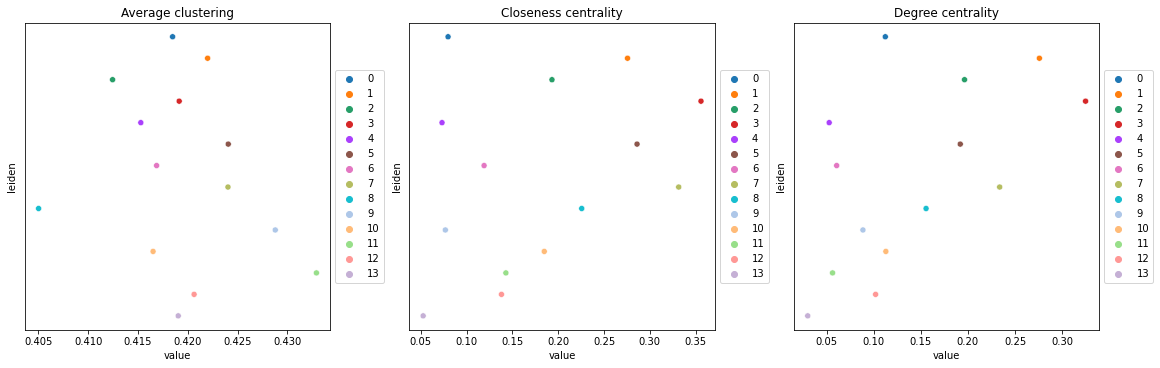
This example shows how to compute centrality scores, given a spatial graph and cell type annotation.
The scores calculated are closeness centrality, degree centrality and clustering coefficient with the following properties:
closeness centrality - measure of how close the group is to other nodes.
clustering coefficient - measure of the degree to which nodes cluster together.
degree centrality - fraction of non-group members connected to group members.
All scores are descriptive statistics of the spatial graph.
This dataset contains Leiden cluster groups’ annotations in anndata.AnnData.obs, which are used for calculation of centrality scores.
First, we need to compute a connectivity matrix from spatial coordinates to calculate the centrality scores. We can use squidpy.gr.spatial_neighbors for this purpose. We use the coord_type="generic" based on the data and the neighbors are classified with Delaunay triangulation by specifying delaunay=True.
sq.gr.spatial_neighbors(adata, coord_type="generic", delaunay=True)
Compute centrality scores
Centrality scores are calculated with squidpy.gr.centrality_scores, with the Leiden groups as clusters.
sq.gr.centrality_scores(adata, cluster_key="leiden")
The results were visualized by plotting the average centrality, closeness centrality, and degree centrality using squidpy.pl.centrality_scores.
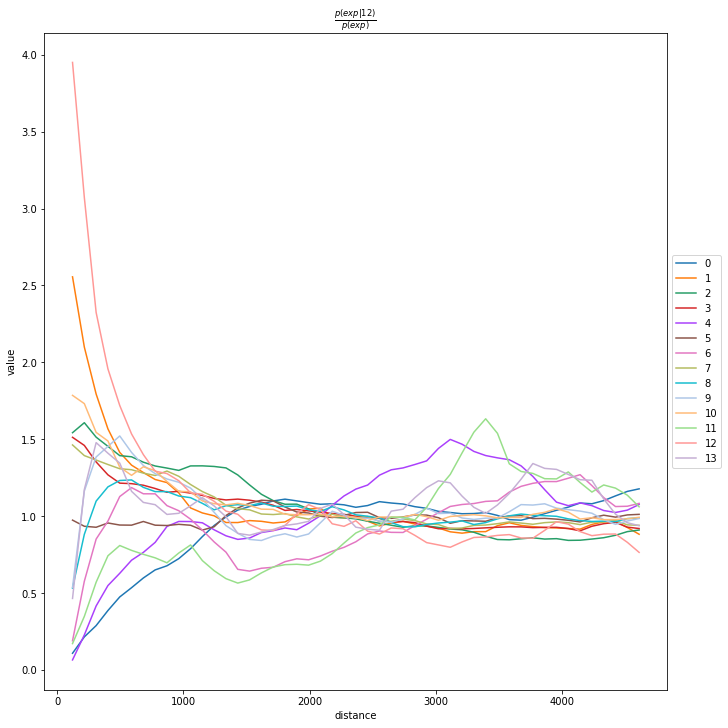
Compute co-occurrence probability
This example shows how to compute the co-occurrence probability.
The co-occurrence score is defined as:
where \(p(exp|cond)\) is the conditional probability of observing a cluster \(exp\) conditioned on the presence of a cluster \(cond\), whereas \(p(exp)\) is the probability of observing \(exp\) in the radius size of interest. The score is computed across increasing radii size around each cell in the tissue.
We can compute the co-occurrence score with squidpy.gr.co_occurrence.
Results of co-occurrence probability ratio can be visualized with squidpy.pl.co_occurrence. The ‘3’ in the \(\frac{p(exp|cond)}{p(exp)}\) represents a Leiden clustered group.
We can further visualize tissue organization in spatial coordinates with squidpy.pl.spatial_scatter, with an overlay of the expressed genes which were colored in consonance with the Leiden clusters.
adata_subsample = sc.pp.subsample(adata, fraction=0.5, copy=True)
sq.gr.co_occurrence(
adata_subsample,
cluster_key="leiden",
)
sq.pl.co_occurrence(
adata_subsample,
cluster_key="leiden",
clusters="12",
figsize=(10, 10),
)
sq.pl.spatial_scatter(
adata_subsample,
color="leiden",
shape=None,
size=2,
)
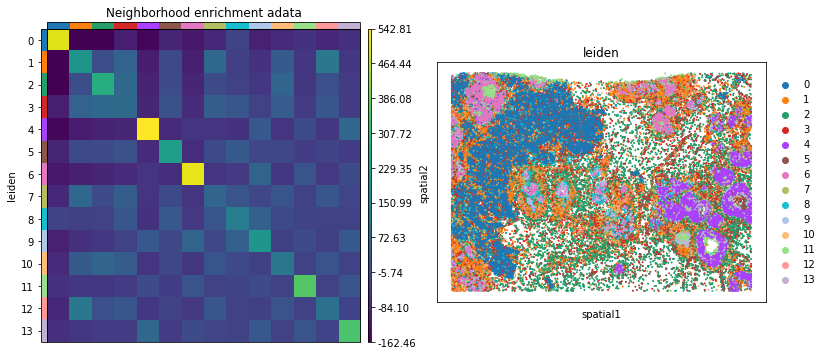
Neighbors enrichment analysis
This example shows how to run the neighbors enrichment analysis routine.
It calculates an enrichment score based on proximity on the connectivity graph of cell clusters. The number of observed events is compared against \(N\) permutations and a z-score is computed.
This dataset contains cell type annotations in anndata.Anndata.obs which are used for calculation of the neighborhood enrichment. We calculate the neighborhood enrichment score with squidpy.gr.nhood_enrichment.
sq.gr.nhood_enrichment(adata, cluster_key="leiden")
100%|██████████| 1000/1000 [00:25<00:00, 38.50/s]
And visualize the results with squidpy.pl.nhood_enrichment.
fig, ax = plt.subplots(1, 2, figsize=(13, 7))
sq.pl.nhood_enrichment(
adata,
cluster_key="leiden",
figsize=(8, 8),
title="Neighborhood enrichment adata",
ax=ax[0],
)
sq.pl.spatial_scatter(adata_subsample, color="leiden", shape=None, size=2, ax=ax[1])
Compute Moran’s I score
This example shows how to compute the Moran’s I global spatial auto-correlation statistics.
The Moran’s I global spatial auto-correlation statistics evaluates whether features (i.e. genes) shows a pattern that is clustered, dispersed or random in the tissue are under consideration.
We can compute the Moran’s I score with squidpy.gr.spatial_autocorr and mode = 'moran'. We first need to compute a spatial graph with squidpy.gr.spatial_neighbors. We will also subset the number of genes to evaluate.
sq.gr.spatial_neighbors(adata_subsample, coord_type="generic", delaunay=True)
sq.gr.spatial_autocorr(
adata_subsample,
mode="moran",
n_perms=100,
n_jobs=1,
)
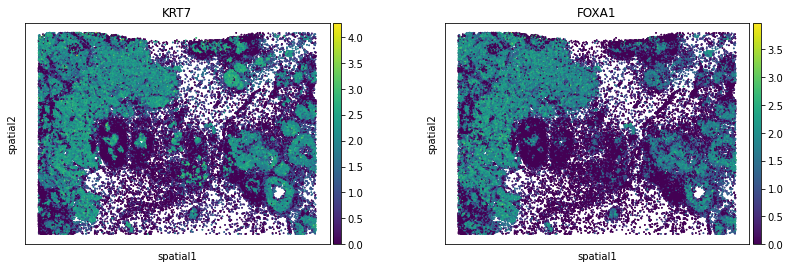
adata_subsample.uns["moranI"].head(10)
100%|██████████| 100/100 [34:39<00:00, 20.80s/]
| I | pval_norm | var_norm | pval_z_sim | pval_sim | var_sim | pval_norm_fdr_bh | pval_z_sim_fdr_bh | pval_sim_fdr_bh | |
|---|---|---|---|---|---|---|---|---|---|
| KRT7 | 0.696668 | 0.0 | 0.000004 | 0.0 | 0.009901 | 0.000008 | 0.0 | 0.0 | 0.009965 |
| SCD | 0.671975 | 0.0 | 0.000004 | 0.0 | 0.009901 | 0.000009 | 0.0 | 0.0 | 0.009965 |
| FOXA1 | 0.659014 | 0.0 | 0.000004 | 0.0 | 0.009901 | 0.000008 | 0.0 | 0.0 | 0.009965 |
| FASN | 0.653400 | 0.0 | 0.000004 | 0.0 | 0.009901 | 0.000006 | 0.0 | 0.0 | 0.009965 |
| EPCAM | 0.641954 | 0.0 | 0.000004 | 0.0 | 0.009901 | 0.000009 | 0.0 | 0.0 | 0.009965 |
| TACSTD2 | 0.638978 | 0.0 | 0.000004 | 0.0 | 0.009901 | 0.000007 | 0.0 | 0.0 | 0.009965 |
| CEACAM6 | 0.631554 | 0.0 | 0.000004 | 0.0 | 0.009901 | 0.000009 | 0.0 | 0.0 | 0.009965 |
| ERBB2 | 0.628083 | 0.0 | 0.000004 | 0.0 | 0.009901 | 0.000009 | 0.0 | 0.0 | 0.009965 |
| KRT8 | 0.619555 | 0.0 | 0.000004 | 0.0 | 0.009901 | 0.000008 | 0.0 | 0.0 | 0.009965 |
| LUM | 0.593700 | 0.0 | 0.000004 | 0.0 | 0.009901 | 0.000007 | 0.0 | 0.0 | 0.009965 |
We can visualize some of those genes with squidpy.pl.spatial_scatter. We could also pass mode = 'geary' to compute a closely related auto-correlation statistic, Geary’s C. See squidpy.gr.spatial_autocorr for more information.