%matplotlib inline
Analyze Merfish data
This tutorial shows how to apply Squidpy for the analysis of Merfish data.
The data used here was obtained from [Moffitt et al., 2018].
We provide a pre-processed subset of the data, in anndata.AnnData format.
For details on how it was pre-processed, please refer to the original paper.
Import packages & data
To run the notebook locally, create a conda environment as conda env create -f environment.yml using this
environment.yml <https://github.com/scverse/squidpy_notebooks/blob/main/environment.yml>_.
import scanpy as sc
import squidpy as sq
sc.logging.print_header()
print(f"squidpy=={sq.__version__}")
# load the pre-processed dataset
adata = sq.datasets.merfish()
adata
scanpy==1.9.2 anndata==0.8.0 umap==0.5.3 numpy==1.21.0 scipy==1.9.3 pandas==1.5.1 scikit-learn==1.1.3 statsmodels==0.13.2 python-igraph==0.10.2 pynndescent==0.5.7
squidpy==1.2.2
100%|██████████| 49.2M/49.2M [00:07<00:00, 7.05MB/s]
AnnData object with n_obs × n_vars = 73655 × 161
obs: 'Cell_ID', 'Animal_ID', 'Animal_sex', 'Behavior', 'Bregma', 'Centroid_X', 'Centroid_Y', 'Cell_class', 'Neuron_cluster_ID', 'batch'
uns: 'Cell_class_colors'
obsm: 'spatial', 'spatial3d'
This datasets consists of consecutive slices from the mouse hypothalamic preoptic region.
It represents an interesting example of how to work with 3D spatial data in Squidpy.
Let’s start with visualization: we can either visualize the 3D stack of slides
using scanpy.pl.embedding():
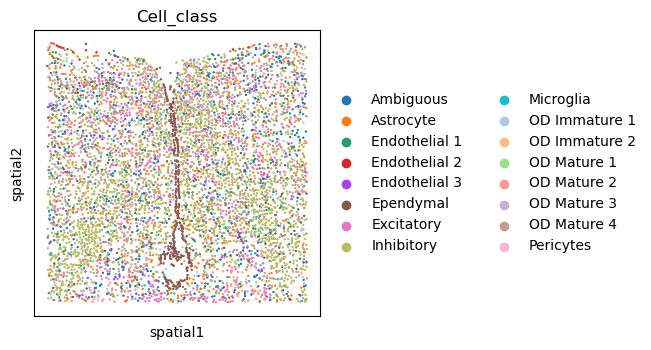
Or visualize a single slide with squidpy.pl.spatial_scatter(). Here the slide identifier
is stored in adata.obs["Bregma"], see original paper for definition.
Neighborhood enrichment analysis in 3D
It is important to consider whether the analysis should be performed on the 3D
spatial coordinates or the 2D coordinates for a single slice. Functions that
make use of the spatial graph can already support 3D coordinates, but it is important
to consider that the z-stack coordinate is in the same unit metrics as the x, y coordinates.
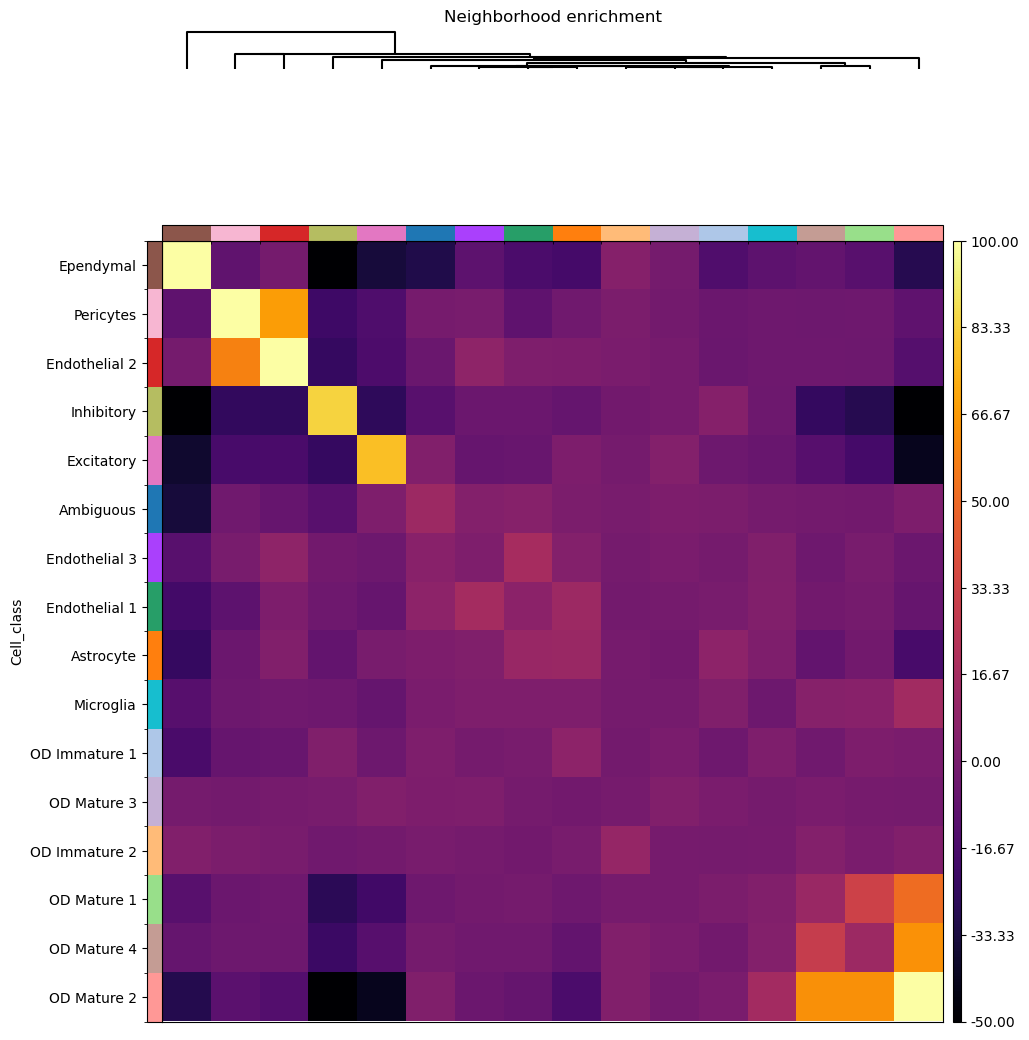
Let’s start with the neighborhood enrichment score. You can read more on the function
in the docs at Building spatial neighbors graph.
First, we need to compute a neighbor graph with squidpy.gr.spatial_neighbors().
If we want to compute the neighbor graph on the 3D coordinate space,
we need to specify spatial_key = "spatial3d".
Then we can use squidpy.gr.nhood_enrichment() to compute the score, and visualize
it with squidpy.gr.nhood_enrichment().
sq.gr.spatial_neighbors(adata, coord_type="generic", spatial_key="spatial3d")
sq.gr.nhood_enrichment(adata, cluster_key="Cell_class")
sq.pl.nhood_enrichment(
adata, cluster_key="Cell_class", method="single", cmap="inferno", vmin=-50, vmax=100
)
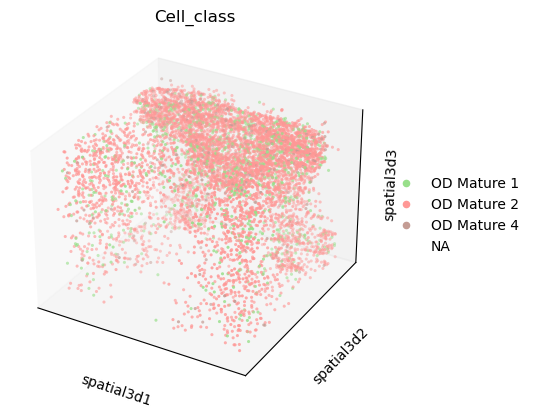
We can visualize some of the co-enriched clusters with scanpy.pl.embedding().
We will set na_colors=(1,1,1,0) to make transparent the other observations,
in order to better visualize the clusters of interests across z-stacks.
sc.pl.embedding(
adata,
basis="spatial3d",
groups=["OD Mature 1", "OD Mature 2", "OD Mature 4"],
na_color=(1, 1, 1, 0),
projection="3d",
color="Cell_class",
)
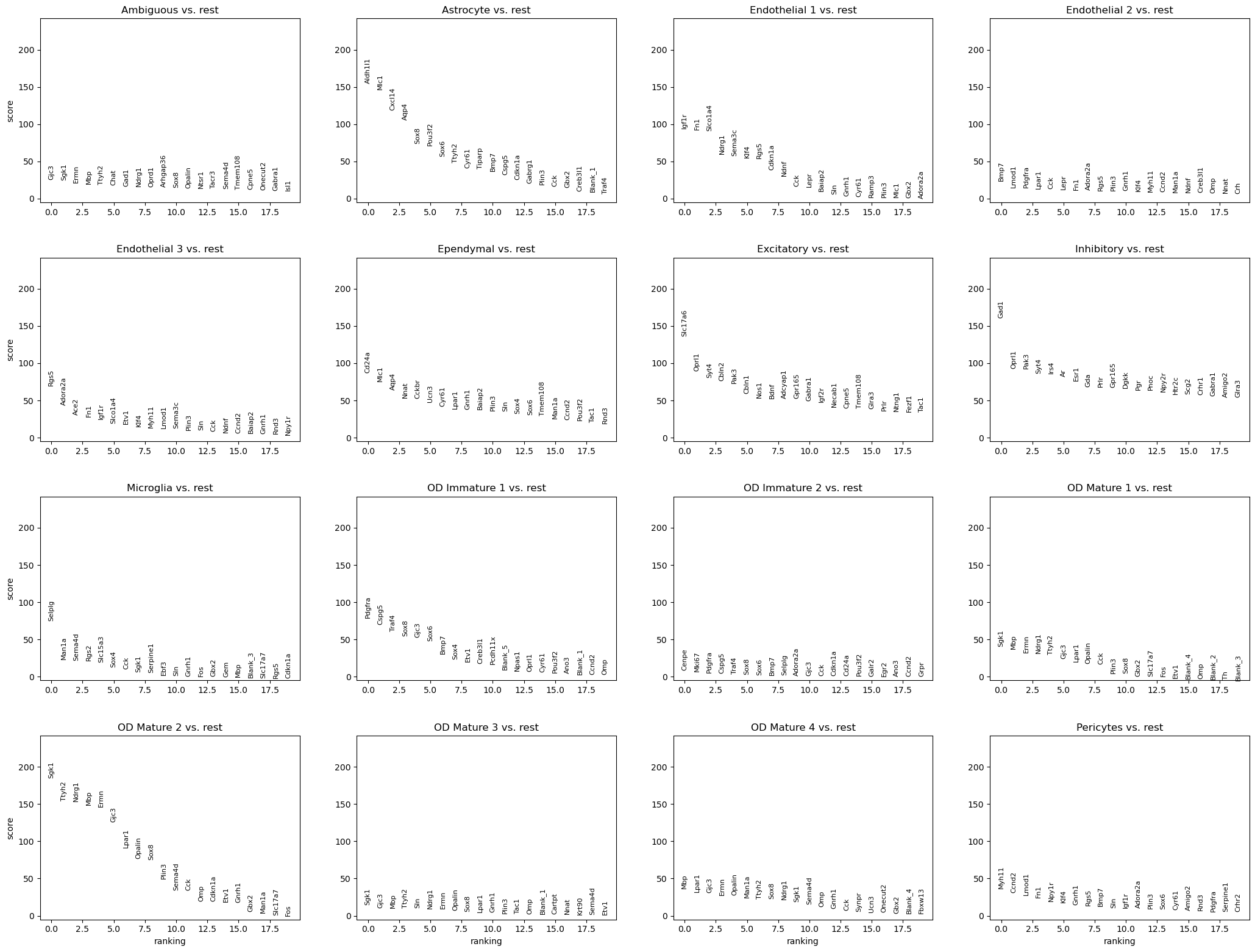
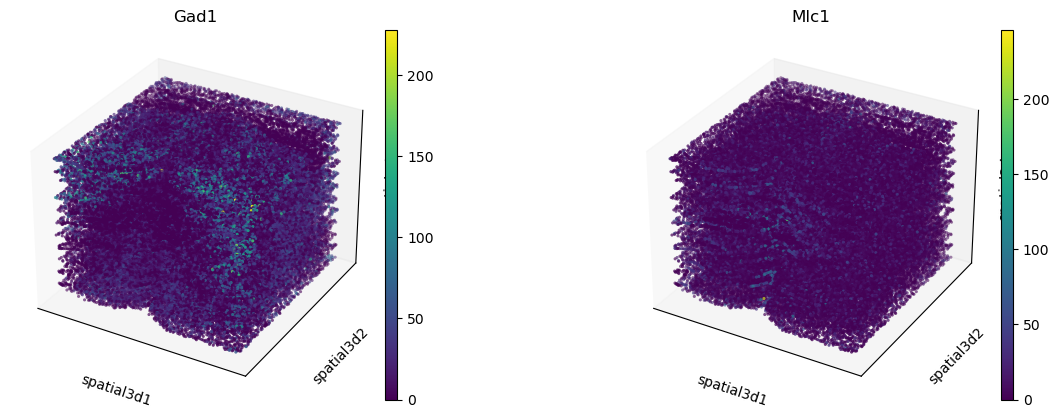
We can also visualize gene expression in 3D coordinates. Let’s perform differential
expression testing with scanpy.tl.rank_genes_groups() and visualize the results
sc.tl.rank_genes_groups(adata, groupby="Cell_class")
sc.pl.rank_genes_groups(adata, groupby="Cell_class")
and the expression in 3D.
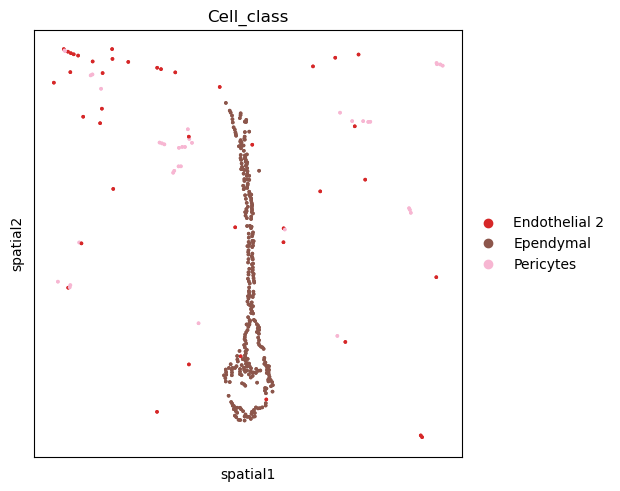
If the same analysis should be performed on a single slice, then it is advisable to
copy the sample of interest in a new anndata.AnnData and use it as
a standard 2D spatial data object.
adata_slice = adata[adata.obs.Bregma == -9].copy()
sq.gr.spatial_neighbors(adata_slice, coord_type="generic")
sq.gr.nhood_enrichment(adata, cluster_key="Cell_class")
sq.pl.spatial_scatter(
adata_slice,
color="Cell_class",
shape=None,
groups=[
"Ependymal",
"Pericytes",
"Endothelial 2",
],
size=10,
)
Spatially variable genes with spatial autocorrelation statistics
With Squidpy we can investigate spatial variability of gene expression.
This is an example of a function that only supports 2D data.
squidpy.gr.spatial_autocorr() conveniently wraps two
spatial autocorrelation statistics: Moran’s I and Geary’s C.
They provide a score on the degree of spatial variability of gene expression.
The statistic as well as the p-value are computed for each gene, and FDR correction
is performed. For the purpose of this tutorial, let’s compute the Moran’s I score.
The results are stored in adata.uns['moranI'] and we can visualize selected genes
with squidpy.pl.spatial_scatter().